Autor: Diviciaco
lunes, 26 de noviembre de 2007
Sección: Escritos antiguos
Información publicada por: diviciaco
Mostrado 39.549 veces.
Dependencia de distancias en el itinerario de Antonino
El análisis de los intervalos entre mansiones mostrará su dependencia lineal respecto a la distancia rectilínea.
Introducción
Hace unos dias comentaba con Abo las dificultades que supone un tipo especial de cálculo de distancias en los itinerarios romanos: la estimación de la distancia entre núcleos, cuando no disponemos de un trayecto completamente definido.
La única solución es confiar en nuestro buen hacer y trazar con el curvímetro un trayecto sobre el mapa, guiados quizá por hitos miliares, cuando existan, y de fragmentos de calzadas y antiguos caminos, confiando en su adscRIPción a la época del itinerario.
Es claro que podemos cometer grandes errores, porque nunca podremos acertar plenamente con el trazado de la vía, aunque lo más grave es que no existirá un sistema claro que justifique y cuantifique lo acertado de nuestro proceder.
Yo sugería aprovechar la ley de los grandes números, y trabajar con un sistema de medias respecto a la distancia en línea recta entre los núcleos. El método es el siguiente:
1 Calculamos la distancia lineal entre cada uno de los puntos del itinerario.
2 Calculamos el porcentaje de variación de la distacia del itinerario con esa distancia lineal
3 Calculamos la media ponderada de esos porcentajes
4 Esa media ponderada, aplicada a la distancia lineal de un punto del itinerario respecto a un núcleo cuya incardinación estemos considerando, nos daría unos kilómetros, que tendremos que comparar con la distancia que figure en el documento romano.
La media ponderada consiste simplemente en aplicar un "peso" a cada uno de los valores, con el objeto de que "puntuen" más en la media los de "peso" mayor, concepto que aquí será la distancia lineal, pues no conviene que puntos muy cercanos, que pueden dar un porcentaje de variación grande pero irrelevante en el conjunto, distorsionen la media.
Una buena descRIPción de esta media la da Wikipedia:
http://es.wikipedia.org/wiki/Media_ponderada
Para este trabajo voy a seguir la sugerencia de Abo, que tengo que agradecerle, de utilizar el itinerario de Antonino.
DescRIPción
a) En concreto voy a utilizar el trayecto nº 1 de ese itinerario, según lo definió Antonio Blázquez, y que puede verse en la página 57, usando los valores de distancia de la columna 1, que finalmente da por válidos:
http://www.cervantesvirtual.com/servlet/SirveObras/12593283118030414198624/p0000001.htm#I_
0_
b) Para la conversión a kilómetros utilizo la milla larga de Blázquez de 1.667 metros.
c) Para las identificaciones de las ciudades y mansiones sigo el Miliario Extravagante, en concreto la página:
http://www.gonzaloarias.net/textos/ciudadmain.htm
d) Para el cálculo de las distancias lineales no utilizo ni curvímetro ni programas como el SIGPAC, para conservar la transparencia del cálculo y garantizar que lo que obtenemos es una pura distancia lineal, que ni siquiera considere los cambios de altitud.
e) El sistema es muy sencillo: la distancia viene definida por la longitud de la hipotenusa de un triángulo cuyos catetos estan conformados por las distancias entre paralelos y meridianos de ambos núcleos.
Obtengo la diferencia entre latitudes y las paso a kilómetros sabiendo que 111,325 kilómetros es un grado. Como la longitudes varía un poco en función del coseno de la latitud no utilizo el valor de latitud de Montero Vítores (aunque la variación es muy pequeña). La fórmula completa de la distancia es la siguiente:
Distancia= RAIZ(((latitud1-latitud0)*60*1.855/1000)^2+((Longitud1-longitud0)* cos(latitud1) *111,325 )^2 )
f) Para obtener las coordenadas utilizo, como de costumbre, esta página:
http://www.heavens-above.com/
Itinerario de Antonino nº 1
En la tabla siguiente (desplegar la primera imagen relacionada) podemos ver, de izquierda a derecha:
http://www.celtiberia.net/imagftp/U2736-grafica.JPG.jpg
1 El nombre de la mansión
2 Las millas
3 El nombre actual
4 La longitud
5 La latitud
6 Las millas pasadas a kilómtros (con la milla larga de Blázquez)
7 La distancia en línea recta
8 El porcentaje de variación de la distancia del itinerario con respecto a la distancia lineal
9 El producto de los kilómetros lineales por el porcentaje, para el cálculo de la media
10 El recálculo de los kilómetros del itinerario, aplicando la media a la distancia lineal
11 El porcentaje de variación de la distancia del itinerario con respecto a la distancia recalculada
Podemos ver que, de 22 distancias analizadas, hay :
17 casos en los que el recálculo de la distancia del itinerario, aplicando el porcentaje medio y la distancia lineal, no difiere más de un 14%
2 casos entre el 15% y el 18% de diferencia
2 casos con hasta el 26% de diferencia
1 caso con el 44,65 % de diferencia
Parece muy evidente la relación de la distancia en línea recta con las millas del itinerario, pero vamos a realizar una prueba de dependencia para salir de dudas.
Para ello utlizaremos una función estadistica, el coeficiente de Pearson (ρ) una prueba que revela el grado de dependencia lineal entre dos conjuntos de datos. Si el coeficiente es próximo a uno la correlación será directa y fuerte, y si es próximo a -1 será inversa y fuerte. -1 < ρ< 1.
En este blog se da una explicación muy sencilla del funcionamiento y aplicaciones de esta función estadística, así como su fórmula:
http://dmgmit.homeip.net/blog/?p=180
Como muestra la gráfica siguiente, se ve una correlación entre la distancia en línea recta y los kilómetros del itinerario, agrupándose los valores en torno a una recta (recta de regresión)

La apreciación visual no basta, en rigor, para determinar esa correlación, pero el coeficiente de Pearson arroja un valor de 0,95254, lo que indica que la correlación es fuerte y directa.
Conclusiones
Hemos demostrado que existe una relación directa y fuerte entre los valores de distancia en línea recta y las millas de este trayecto del itinerario de Antonino.
En consecuencia con ello hemos comprobado que las distancias que nos da el itinerario responden a un porcentaje medio sobre la distancia en línea recta, obteniéndose difererencias razonables en la mayoría de los casos.
Esta vinculación entre las millas de este itinerario y la distancia en línea recta, puede establecerse por medio de una fórmula aproximativa, válida para la mayoría de los casos:
Millas Itinearario = (100/80,46) x Distancia en línea recta / 1,667
El resultado práctico de esto es que podemos analizar la parte segura de un itinerario, a ser posible con las medidas anteriores y posteriores al tramo en duda, y aplicando la fórmula sobre un lugar que sospechemos se incardina en el trayecto podremos incluirlo o rechazarlo, cuantificando exáctamente las posibilidades de acierto y de error, en función del número de recálculos positivos que habremos efectuado sobre la parte conocida del itinerario, lo que ofrece un vivo contraste con las conjeturas de los métodos planimétricos.
No obstante, evidentemente, no pretendo substituir el análisis de las vías romanas, ni mucho menos los trabajos arqueólogicos, sino sólamente ofrecer una primera aproximación, ofreciendo un rango de coordenadas válido para desarrollar estos esfuerzos.
Comentarios
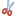 Pulsa este icono si opinas que la información está fuera de lugar, no tiene rigor o es de nulo interés.
Pulsa este icono si opinas que la información está fuera de lugar, no tiene rigor o es de nulo interés.
Tu único clic no la borarrá, pero contribuirá a que la sabiduría del grupo pueda funcionar correctamente.
Si te registras como usuario, podrás añadir comentarios a este artículo.


No hay más información.
...0