Autor: Diviciaco
viernes, 26 de octubre de 2007
Sección: Historia Antigua
Información publicada por: diviciaco
Mostrado 21.255 veces.
Crítica a los ejes de referencia establecidos por Jeromor para la ubicación de Titulcia
Se discute el citado eje de referencia y se establecen unas fórmulas de declinación para ese cuadrante.
Introducción
Jeromor establece en su artículo sobre la situación de Titulcia un eje referencial entre Toledo y el lugar de El Juncal para ubicar la ciudad de Titulcia, en un sistema de coordenadas declinado 13º, haciendo una crítica al eje de referencia Toledo -El Viso propuesto por Jesús Montero Vitores, por causa de la ubicación de Complutum
Vamos a ver si el sistema propuesto por Jeromor es válido. No voy a entrar en si la ubicación de Complutum estaba en tal o cual lugar sino a comprobar si su sistema es formalmente válido. Para ello voy a trabajar con resultados numéricos y algebráicos, más objetivables, en vez de con cuadrícula. Como primer paso deduciremos unas fórmulas de declinación para ese cuadrante:
Fórmulas de declinación
Podemos ver como evoluciona la distancia entre paralelos declinados (DT) en función de las distancias reales entre los paralelos y meridianos entre el centro de referencia y el punto P
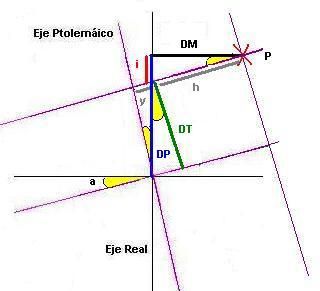
En el gráfico podemos obtener la distancia entre paralelos declinados (DT):
i=DM x Tag(a)
DT=cos(a) x (DP - i)
DT= cos(a) x (DP-(DM x tag(a)))
o bien:
DT= DP x cos(a) - DM x sen(a)
Análogamente obtenemos la distancia entre meridianos declinados (GT)
h=DM/cos(a)
y=sen(a) x (DP-i)
GT=h + y
GT=(DM/cos(a)) + sen(a) x (DP- (DM x tag(a)))
Análisis del eje de referencia Toledo - Cerro del Viso propuesto por Jesús Montero Vítores
Toledo
Latitud real = 39º 52' = 39,86666º
Longitud real = 4º 02' = 4,03333º
Toletum
Latitud ptolemaica = 41º
Longitud ptolemaica = 10º
Cerro del Viso
Latitud real = 40º 28' = 40,46666º
Longitud real = 3º 23' = 3,383333º
Complutum
Latitud ptolemaica = 41º 30'
Longitud ptolemaica = 11º
Distancia entre las latitudes reales:
DP = 40,46666-39,86666 = 0,6 x 60 =36' x 1.851 = 66,63 km
Distancia entre las longitudes reales
DM=4,03333-3,383333=0,649997 x 60 = 38,99982' x 1350 = 52,649 km
Distancia entre las latitudes ptolemaicas
DT' = 41º 30' - 41º = 30' ; 30' x 1.540 = 46,2 km
Distancia entre las longitudes ptolemaicas
DG' = 11º - 10º = 1º ; 60' x 1.123 =67,38 km
Aplicamos las fórmulas de declinación para este cuadrante:
DT= cos(a) x DP - DM x sen(a)
DT= cos(13) x 66,63 - 52,649 x sen(13)=53,08 km
GT=(DM/cos(a)) + sen(a) x (DP- (DM x tag(a)))
GT =(52,649 / cos(13)) + sen(13) x (66,63 - (52,649 x tag(13)))) =66,29 km
La diferencia de distancias entre los paralelos ptolemaicos y los que hemos obtenido declinando 13º es:
DT - DT' = 7,06 km
Entre meridianos el ajuste es mucho mejor.
GT - GT' = 1,09 km
Aunque llama la atención que se haya buscado un mejor ajuste en longitud que en latitud, donde la diferencia se lleva al límite aceptable, DT se corresponde con DT' por ser inferior la diferencia a 5 minutos de grado, de acuerdo a toda la metodología propuesta; por tanto el eje de referencia es válido.
El ajuste perfecto de latitudes sólo se consigue abriendo los ejes hasta los 18,7 grados.
La declinación a 13 º sigue siendo válida aún utilizando las coordenadas más precisas de Toledo que propone Jeromor.
Análisis del eje de referencia Toledo - El Juncal propuesto por Jeromor
Toledo
Latitud real = 39º 51' 30'' = 39,85833º
Longitud real = 4º 02' 40'' = 4,04444º
Toletum
Latitud ptolemaica = 41º
Longitud ptolemaica = 10º
El Juncal
Latitud real = 40º 28' 40'' = 40,4777º
Longitud real = 3º 24' 40'' = 3,4111º
Complutum
Latitud ptolemaica = 41º 30'
Longitud ptolemaica = 11º
Distancia entre las latitudes reales:
DP = 40,4777-39,85833 =0,61937 x 60 =37,1622' x 1.851 =68,79 km
Distancia entre las longitudes reales
DM= 4,04444 - 3,4111=0,63334 x 60 = 38,0004' x 1350 = 51,30 km
Distancia entre las latitudes ptolemaicas
DT' = 41º 30' - 41º = 30' ; 30' x 1.540 = 46,2 km
Distancia entre las longitudes ptolemaicas
DG' = 11º - 10º = 1º ; 60' x 1.123 =67,38 km
Aplicamos las fórmulas de declinación para este cuadrante:
DT= cos(a) x DP - DM x sen(a)
DT= cos(13) x 68,79 - 51,30 x sen(13)=55,49 km
GT=(DM/cos(a)) + sen(a) x (DP- (DM x tag(a)))
GT =(51,30 / cos(13)) + sen(13) x (68,79 - (51,30 x tag(13)))) =65,46 km
La diferencia de distancias entre los paralelos ptolemaicos y los que hemos obtenido declinando 13º es:
DT - DT' = 9,47 km
y entre meridianos:
GT - GT' = 1,92 km
Conclusión
El ajuste entre paralelos no se ha conseguido con una declinación de 13º pues la diferencia de latitudes es superior a 6 minutos de grado y por tanto inaceptable de acuerdo al intervalo de coordenadas de Ptolomeo, establecido en 5º, y de acuerdo a la metodología propuesta, también utilizada por Jeromor.
Por todo ello procede rechazar el sistema de referencia propuesto por Jeromor para localizar la ciudad de Titulcia.
Enlaces
Carpetanos y vettones en la Hispania de Ptolomeo: Ciudades y vías romanas de Carpetania y Vettonia de Jesús Montero Vitores (2000).
http://www.ucm.es/eprints/2317/
La ubicación de la Intercatia vaccea: propuesta de solución desde la geografía de Ptolomeo
http://www.celtiberia.net/articulo.asp?id=2905
Situación de Titulcia
http://www.celtiberia.net/articulo.asp?id=2908
No hay imágenes relacionadas.
Comentarios
 Pulsa este icono si opinas que la información está fuera de lugar, no tiene rigor o es de nulo interés.
Pulsa este icono si opinas que la información está fuera de lugar, no tiene rigor o es de nulo interés.
Tu único clic no la borarrá, pero contribuirá a que la sabiduría del grupo pueda funcionar correctamente.
Si te registras como usuario, podrás añadir comentarios a este artículo.

Hay 1 comentarios.
1