Autor: Diviciaco
jueves, 07 de febrero de 2008
Sección: Historia Antigua
Información publicada por: diviciaco
Mostrado 47.030 veces.
La clave de Ptolomeo: Transformaciones de latitud y longitud para Hispania.
Donde se proporcionan las fórmulas de transformación de las latitudes y de las longitudes ptolemaicas en reales.
La latitud
La tabla IV(1) de J. Montero Vítores y Martinez Hombre, de equivalencia de latitudes ptolemaicas y reales para Hispania se calculaba de la siguiente forma:
a Comenzando por el paralelo 36º, coincidente en la geografía de Ptolomeo y en la actual, vamos subiendo hacia el paralelo 45º, obteniendo las diferencias con el paralelo 36º.
b Cada diferencia la multiplicamos por el valor de un grado (91,354 km) en la tierra de Posidonio.
c Se obtiene la razón con el grado de latitud real (111,11 km)
d A este valor se le suman los 36º y nos da la equivalencia que que trasladamos a la tabla.
Esta tabla permite obtener unas equivalencias de latitudes con las que se pueden obtener buenos resultados a la hora de interpretar la Geographia de Ptolomeo.
Esta tabla, al ser obtenida por un método uniforme podemos convertirla en una fórmula sin más que seguir, tal cual, los pasos del procedimiento de Martínez Hombre y así obtenemos nuestra primera transformación:
Latitud Real = 36 + (Latitud Ptolomeo - 36) x 91,354 / 111,11
En efecto, veamos lo que ocurre si queremos saber la latitud real de Lucus Asturum, indicada con 45º en las tablas de Ptolomeo:
Latitud real = 36 + (45 -36) x 91,354 /111,11 =43,399º =43º 23,94'
La latitud de Sta María de Lugo es de 43,43938º=43º 26,36' difieriendo con la obtenida en sólo 2 minutos reales, cuyo valor en km está dentro del rango de los 5' con que trabajaba Ptolomeo.
Además podemos calcular la inversa de la fórmula y así obtener las coordenadas de Ptolomeo que corresponderían con unas coordenadas reales.
Latitud Ptolomeo=( (Latitud Real x 111,11) - 711,16) / 91,354
que aplicadas al caso anterior obtenemos: Latitud Ptolomeo=45,0480º=45º 2,8', con la diferencia de dos minutos ptolemaicos, que otorga validez al resultado.
Si aplicamos esta fórmula a Toledo, con una latitud real de 39,8670º obtenemos:
Latitud Ptolomeo=40,7032º=40º 42,19', siendo Líbora con 40º 45' el único núcleo cuya latitud cuadraría en las tablas con este resultado, dentro del margen de los 5', coincidente con el obtenido en mi artículo http://www.celtiberia.net/articulo.asp?id=2961 , a partir de la latitud de Cauca y coincidente también con las coordenadas alternativas para Toletum, que daba J. Montero en la página 334 de su tesis.
Como estas funciones producen un continuum de valores para Hispania (como dicen los matemáticos son continuas en el intervalo), ya no es necesario adaptar los valores a la tabla IV, sino que basta aplicar la fórmula para conseguirlo: así al contener la tabla, pero además trascenderla, podemos jubilar tranquilamente la tabla IV, después de rendir tan inestimables servicios.
La longitud
No existe un meridiano que coincida en la Geographia y en la realidad, tal y como ocurre con la latitud, que coinciden los paralelos 36º, sino que además las longitudes presentan variaciones importantes a medida que nos desplazamos de oeste a este, de modo que estamos ante un problema importante.
De todas formas Martínez Hombre obtuvo unos valores del grado de longitud en kilómetros, para cada latitud, que pueden verse en la tabla IV de la tesis de J. Montero.
Claudioptolomeo en su artículo de Celtiberia Una revisión de cálculos para las coordenadas de la Carpetania en la Geographia de Ptolomeo http://www.celtiberia.net/articulo.asp?id=3012 propone, para minimizar el problema de la longitud, usar el valor de grado de longitud (para cada paralelo) con respecto a un meridiano local (diferencia de longitudes), y aplicar esa diferencia sobre el meridiano real, teniendo en cuenta su variación de valor de grado de longitud real con respecto a la latitud real.
Aquí se planteó un problema, pues al utilizarse para 39º 59' el mismo minuto de longitud real que para 35º, usando los valores puntuales de la tabla de A. Strahler, que da para 35º 91,290 km y para 40º 85,397 km, se genera un error de unos 20'.
Evidentemente el valor de grado de longitud no fluctúa a saltos, sino que es una función continua de la latitud, y para 39º 59' el valor ya es, prácticamente, el de 40º y no el de 35º.
Puede calcularse muy precisamente para la tierra por medio de la fórmula del elipsoide, forma real de nuestro planeta, obteniéndose los valores de la tabla de A. Strahler.
Como esta fórmula es algo engorrosa, casi siempre se utiliza la fórmula del coseno (que supone una tierra esférica) que genera valores cuyas discrepancias con las del elipsoide son irrelevantes para nuestra aplicación.
Esta es la fórmula del valor de grado la longitud real:
Valor de longitud 1º real = Cos(latitud real) * 111,325
Los 111,325 km son el valor del grado de latitud en el ecuador, que es más dilatado.
Estos son algunos de los valores que podemos obtener con dicha fórmula:
Latitud = 35,0 Kilómetros 1º Longitud = 91,192
Latitud = 36,0 Kilómetros 1º Longitud = 90,064
Latitud = 37,0 Kilómetros 1º Longitud = 88,908
Latitud = 38,0 Kilómetros 1º Longitud = 87,725
Latitud = 39,0 Kilómetros 1º Longitud = 86,516
Latitud = 39,9 Kilómetros 1º Longitud = 85,405
Latitud = 40,0 Kilómetros 1º Longitud = 85,280
Vemos que la discrepancia con el valor del elipsoide no tiene ninguna importancia para la mayoría de las aplicaciones, ni desde luego para la nuestra, como vemos para el valor de 40º de la tabla de A. Strahler: 85,397-85,280 = 117 metros de diferencia, que nos ahorran la aplicación de una fórmula compleja o la consulta de las tablas, donde hemos visto que podemos cometer errores.
Bien, pero ¿y el grado de longitud de Ptolomeo?
Pues resulta que figura en la tabla IV y habíamos prometido jubilarla, así que vamos a ver si lo logramos:
Podríamos hacer una regresión sobre los valores de la tabla IV y obtener la recta que nos daría ya la función de longitud, este método es perfectamente válido y he comprobado que produce un excelente resultado, pero prefiero atacarlo de otra forma algo diferente, para que la fórmula obtenida no pierda información sobre el comportamiento trigonométrico de las longitudes, que puede sernos útil en el futuro:
El grado de longitud tiene que variar en función del coseno en la tierra de Posidonio aún mejor que en la tierra real, pues aquella es una esfera perfecta. Esto ha de considerarse como rigurosamente cierto, pues de otra manera no existiría base matemática alguna para la Geographia.
Podríamos hacer esta primera aproximación:
Valor de longitud 1º de Ptolomeo = Cos(latitud ptolomeo) x 92,406
siendo 92,406 el valor del grado de latitud.
Ahora bien, vemos que el valor de latitud no concuerda, analizando el primer valor de la tabla, que para 45º 40' son 61,616 km de longitud:
61,616=Cos(45,666) x Vgrado; Vgrado=61,616/cos(45,666); Vgrado=88,17 <> 92,406
Repitiendo este proceso para unos cuantos valores espaciados:
45º 40' 61,616 88,17003303
44º 50' 62,39 87,97724131
43º 30' 63,498 87,53824582
42º 20' 64,459 87,19637731
41º 50' 64,879 87,07560883
40º 10' 66,279 86,73315831
39º 25' 66,909 86,60810927
38º 30' 67,679 86,47878176
37º 45' 68,309 86,3916792
36º 15' 69,559 86,25390961
Esto es una sorpresa, pues supone que se utilizó un valor de grado de latitud distinto en cada paralelo para calcular cada valor de longitud, cuando el valor de grado de latitud debiera de ser constante.
Martínez Hombre calculó sus valores sobre la península ibérica, sumando 0,0070 hasta los 42º 40' y llevando J. Montero estos valores hasta los 36º
La media de este valor de grado es de: 87,0423 con lo cual obtenemos nuestra segunda aproximación de longitud:
Valor de longitud 1º de Ptolomeo = Cos(latitud ptolomeo) x 87,0423
Esta es la fórmula que daba en los comentarios del artículo de Claudioptolomeo, pero podemos ir más allá y hacerla completamente exacta:
Si representamos los valores de latitud recalculados en función del coseno contra el grado de latitud ptolemaico en el diagrama de dispersión que se presenta, vemos que hay una relación lineal entre ambos, que responde a un coeficiente de Pearson de 0,9814127, que indica una correlación muy fuerte entre ambos conjuntos de datos.
Podemos, entonces, hacer una regresión lineal y sacar la recta que los relaciona, que es como sigue:
Vgrado' =0,2111702175614171 x Latitud + 78,3790669888567
Vemos algo muy interesante: la pendiente de la recta es 0,21117 y la pendiente es, como se sabe, la tangente del ángulo de la recta. Si ahora calculamos el arcotangente nos da un ángulo de 12º. Este ajuste del grado de latitud para la longitud es consecuencia de la proyección cónica Mercator.
Si ahora recalculamos los valores, vemos que las diferencias son insignificantes, luego ya tenemos como varía este grado de latitud en la tabla de longitudes de Martínez Hombre y J. Montero.
Latitud Vgrado Vgrado' Diferencia
45,66666667 88,17003303 88,02250692 0,147526111
44,83333333 87,97724131 87,84653174 0,130709567
43,5 87,53824582 87,56497145 -0,026725634
42,33333333 87,19637731 87,3186062 -0,12222889
41,83333333 87,07560883 87,21302109 -0,137412262
40,16666667 86,73315831 86,86107073 -0,127912421
39,41666667 86,60810927 86,70269306 -0,09458379
38,5 86,47878176 86,50912036 -0,030338605
37,75 86,3916792 86,3507427 0,040936496
36,25 86,25390961 86,03398738 0,219922232
Recalculando los valores de longitud de la tabla IV con Vgrado'
Km Recálculo Mts diferencia
61,616 61,5129041 -0,103095899
62,39 62,29730592 -0,092694085
63,498 63,51738609 0,01938609
64,459 64,54935641 0,090356415
64,879 64,98138424 0,102384241
66,279 66,37674701 0,097747015
66,909 66,9820706 0,073070604
67,679 67,70274324 0,02374324
68,309 68,27663194 -0,032368061
69,559 69,3816449 -0,177355097
Vemos que las diferencias son inapreciables, y así hemos conseguido nuestro objetivo de cristalizar en una fórmula todos los valores de longitud de la tabla IV. Ahora vamos a intentar obtener con estos datos una transformación de la longitud:
De acuerdo a esta fórmula, la distancia entre dos núcleos de la Geographia de longitudes lgp1 y Lgp0 y latitud Ltp sería:
Distancia= (Lgp1-Lgp0) x Cos(Ltp1) x (0,2111702175614171 x Ltp1 + 78,3790669888567)
Si la divido por la distancia real, de los mismos puntos con latitudes Lt1 y Lt0, obtendré grados reales:
Gradosr= (Lgp1-Lgp0) x Cos(Ltp1) x (0,2111702175614171 x Ltp1 + 78,3790669888567)/ Cos(Latitudreal) x 111,325
calculando la diferencia con la longitud real de referencia obtendremos la longitud real y la última de nuestras transformaciones:
Longitud real = |((Lgp1-Lgp0) x Cos(Ltp) x (0,2111702175614171 x Ltp1 + 78,3790669888567)/ Cos(Latitudreal) x 111,325 ) - Longitud_real_referencia|

Para probar la fórmula de la longitud, vamos a hacer la misma prueba que Martínez Hombre:
Calcularemos la distancia entre los cabos Higuer y Ortegal, que deberá corresponderse con la distancia entre el Trileucum y el Promontorio Oeasso:
1 Promontorio Trileucum (cabo Ortegal)
Longitud 8º 15' = 8,25º pt
Longitud 7,8767º r
2 Promontorio Oeasso (Higuer)
Latitud 45º 50' = 45,8333º pt
Longitud 15º 10' = 15,1666º pt +1º (Existe un grado suprimido)
Latitud 43,39208º r
Longitud 1,79214º r
Longitud real = |( (16,1667º - 8,2500º) x Cos(45,8333º) x (0,21117 x 45,8333º + 78,379) / (Cos(43,39208º ) x 111,325) ) - 7,8670º| = 1,86284º = 1º 51,7º
1,86284º-1,79214º=0,0707º=4,242' unos 5,7 km, un resultado aceptable en el entorno de los 5' ptolemaicos.
Puede precisarse más el resultado si consideramos que el valor más alto de latitud en la tabla IV de Martínez Hombre y Montero Vítores es de 45º 45'.
Por esta razón y como los valores de latitud del litoral cantábrico están fuertemente exagerados en la Geographia, podemos usar para estos promontorios ese valor máximo de latitud 45º 45' o 45,75º (2)
Longitud real = |( (16,1667º - 8,2500º) x Cos(45,75º) x (0,21117 x 45,75º + 78,379) / (Cos(43,39208º ) x 111,325) ) - 7,8670º| = 1,8551º = 1º 51,3º
1,8551º-1,79214º=0,06296º=3,77' unos 5 km, dentro del rango de 5' Ptolemaicos, el resultado es bueno.
Ahora bien: es posible precisar aún más este resultado, hasta el punto de hacerlo completamente perfecto, si calculamos la latitud real y utilizamos el valor obtenido para alimentar la fórmula de la longitud:
Latitud real = 36º + (45,8333º - 36º) x 91,354 / 111,11 = 44,0849º = 44º 5,09'
Vemos que la latitud no coincide, por la exageración septentrional. No nos importa, pues ahora estamos probando la fórmula de la longitud:
Longitud real = |( (16,1667º - 8,2500º) x Cos(45,8333º) x (0,21117 x 45,8333º + 78,379) / (Cos(44,0849º) x 111,325) ) - 7,8670º| = 1,7929º = 1º 47,57'
Vemos como el resultado es correcto, correspondiéndose con toda exactitud con la longitud del cabo Higuer.
El cálculo es, asimismo, adecuado para Lucus Asturum a mitad de camino:
45º 11º ' Coord. de: Lucus Asturum (45,0000º , 11,0000º)
Latitud real = 36º + (45,0000º - 36º) x 91,354 / 111,11 = 43,3997º = 43º 23,98'
Longitud real = |( (11,0000º - 8,2500º) x Cos(45,0000º) x (0,21117 x 45,0000º + 78,379) / (Cos(43,3997º) x 111,325) ) - 7,8670º| = 5,7543º = 5º 45,26'
El dato real es (43º 26' 5º 49')r
Este será el proceder a partir de ahora: se calculará la latitud real con la primera transformación, y ese valor se usará para calcular la longitud con la segunda transformación.
(1)
(2)
En realidad se puede "bajar" aún más la latitud, hasta los 45º 5' de Oeasso:
http://www.ucm.es/eprints/2317/ pag 116
Comprobación
Voy a hacer que la fórmula recalcule el valor del punto 8 de Claudioptolomeo Una revisión de cálculos para las coordenadas de la Carpetania en la Geographia de Ptolomeo http://www.celtiberia.net/articulo.asp?id=3012 para demostrar la absoluta identidad entre la fórmula y la tabla de longitudes.
Escojo este punto, porque el grado de longitud que utiliza aquí es bueno:
En el paralelo 41º 05´ N el grado de longitud real es de 85, 397 Kms ( 1´= 1.423 mts)
En realidad 41º 05' es la latitud ptolemaica, siendo la real 40º 11', que con la fórmula del coseno le corresponden: cos(40.18333º) x 111,325 = 85,050 km.
Vemos que a pesar de usar Claudioptolomeo la latitud de Ptolomeo en vez de la real para buscar en la tabla, no hay error -unos cientos de metros-, pues usó el valor de 40º de la tabla, pero es ilustrativo de los continuos problemas y el engorro que suponen el manejo repetitivo de tablas.
PUNTO 8. 41º 05', 10º 50'
1 Complutum (Cerro del Viso)
- Latitud real 40º 27' = 40,45º
- Longitud real 3º 22' = 3,366º (en realidad el Cerro del Viso está a 3º 24')
- Latitud Ptolomeo 41º 20' = 41,3333º
- Longitud Ptolomeo 10º 20' = 10,3333º
2 Punto 8
- Latitud real 40º 11' = 40,18333º
- Latitud Ptolemaica 41º 05' = 41,083333º
- Longitud Ptolemaica 10º 50' = 10,83333º
|( (10,83333 - 10.33333) x Cos(41,083333) x (0,211170217561417 x 41,0833333 + 78,3790669888567) / (Cos(40,183333) x 111,325) ) - 3,36666 |= 2,9809º = 2º 58,85'
Estos 2º 58,85' son el mismo resultado obtenido por Claudioptolomeo:
40º 11´ N , 2º 59 ´W = Leganiel /sur de Driebes.
Vemos como gracias a las barras de los valores absolutos nuestra fórmula es inteligente y sabe si tiene que restar o sumar el desplazamiento, entregando limpamente la coordenada de longitud.
Conclusiones
Hemos conseguido expresar tanto las transformaciones de latitud como de la longitud como funciones matemáticas. También hemos demostrado la operatividad de dichas funciones, llevando su precisión hasta el punto de operar con los valores de grado de longitud para cada latitud. Y ello tanto para la longitud real como la ptolemaica.
La regularidad subyacente a los valores de longitud de Martínez Hombre y J. Montero, la respuesta a los valores del coseno, ha sido un descubrimiento que me ha llenado de emoción y de confianza en una resolución final del problema de la longitud.
Podría haber utilizado un sistema más sencillo, como hacer una recta de regresión que me diese los valores de grado longitud en función de la latitud ptolemaica, de hecho lo intenté y obtuve excelentes resultados. Para quien le interese:
Grado Longitud Ptol= -0,81107906 x Latitud + 98,7322
Pero así nos iríamos a una fórmula plana y perderíamos la información que ha aportado el análisis: que la longitud de Ptolomeo varía, como corresponde a una verdadera geografía, según el coseno de la latitud, y que las correcciones introducidas por los autores de referencia implican un grado de latitud variable, asociado a una recta de 12º, consideraciones que requieren un análisis más profundo.
La expresión de estas fórmulas implica algo mucho más trascendente que la comodidad que puedan reportar a la hora de hacer cálculos con las coordenadas de la Geographia: podemos estudiar ahora el comportamiento de estas funciones y buscar regularidades que nos ayuden a perfeccionarlas más y más: la Geographia es ahora más vulnerable al arsenal matemático y más susceptible de análisis, como el informático, de manera que la resolución completa de sus problemas no está ya muy lejana.
Enlaces
Carpetanos y vettones en la Hispania de Ptolomeo: Ciudades y vías romanas de Carpetania y Vettonia de Jesús Montero Vitores (2000).
http://www.ucm.es/eprints/2317/
La ubicación de la Intercatia vaccea: propuesta de solución desde la geografía de Ptolomeo.
http://www.celtiberia.net/articulo.asp?id=2905
También utilizé el Sigpac:
http://sigpac.mapa.es/fega/visor/
Las tablas de Ptolomeo fueron consultadas en esta dirección:
http://penelope.uchicago.edu/Thayer/E/Gazetteer/Periods/Roman/_Texts/Ptolemy/2/5*.html
Este artículo mio en Celtiberia prosigue con la identificación de núcleos vacceos, siguiendo el mismo procedimiento:
http://www.celtiberia.net/articulo.asp?id=2916
En otro de mis artículos de Celtiberia se obtienen las fórmulas de declinación para el 2º cuadrante:
http://www.celtiberia.net/articulo.asp?id=2918
Aquí situo algunos puntos de Asturias
http://www.celtiberia.net/articulo.asp?id=2946
La Carpetania con respecto al paralelo ptolemaico de Cauca. El caso de Titulcia
http://www.celtiberia.net/articulo.asp?id=2961
Revisión de la situación de Titulcia, de acuerdo al itinerario 24 de Antonino
http://www.celtiberia.net/articulo.asp?id=3003
Claudioptolomeo Una revisión de cálculos para las coordenadas de la Carpetania en la Geographia de Ptolomeo
http://www.celtiberia.net/articulo.asp?id=3012
Conversor ON LINE de coordenadas ptolemaicas para Hispania
Aquí se puede enlazar un conversor automático de coordenadas:
Para usarlo hay que meter la longitud real de un punto de referencia conocido para el territorio a analizar, por ejemplo Lugo: 7º 33'
Luego hay que meter la longitud de referencia que creemos se corresponde con ese lugar en Ptolomeo, por ejemplo los 6º 25' de Iria Flavia (las coordenadas y el nombre no tienen porque coincidir en las listas de Ptolomeo, debido a las alteraciones medievales y renacentistas)
Y ya sólo queda meter las coordenadas de Ptolomeo para saber por donde caen. Por ejemplo probad con los 45º 5º 20' de Portus Artabri
Nos dará las coordenadas reales en formato decimal Y UN ENLACE PARA VOLAR DIRECTAMENTE AL LUGAR CON GOOGLE EARTH
Comentarios
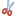 Pulsa este icono si opinas que la información está fuera de lugar, no tiene rigor o es de nulo interés.
Pulsa este icono si opinas que la información está fuera de lugar, no tiene rigor o es de nulo interés.
Tu único clic no la borarrá, pero contribuirá a que la sabiduría del grupo pueda funcionar correctamente.
Si te registras como usuario, podrás añadir comentarios a este artículo.

nepocianus29 de nov. 2007La verdad Diviciaco sigues sorprendiéndonos con tu saber y el rigor con que expones las cosas. Eres todo un referente. Perdona que aunque no tenga que ver con tu artículo te he mandado hace unos dias una pregunta acerca de la presencia ligur e iliria en la Península Ibérica cuestión muy debatida y que cuanto mas me enfrasco en ella menos cosas claras tengo no se si te habrá llegado la cuestión o no has tenido tiempo de responderme pero aguardo con impaciencia alguna orientación tuya muchas gracias.
Excelente trabajo. ¿Podíamos conocer según este método las coordenadas de Laminion según los diferentes códices?
Son:
10º 50' 39º 55' (la usual)
10º 50' 39º 45'
13º 39º 40'
13º 39º 45'
10º 20' 39º 55'
10º 20' 39º 45'
10º 20' 39º 40'
Muchas gracias
¡Ya sé que tengo muchas preguntas para contestar, pero es que no puedo de momento!
Os prometo que en breve os responderé a todos, de verdad.!
Gracias diviciaco, no tengo prisa. Estoy interesado en el tema por este motivo
http://villarrobledohistorico.blogspot.com/2007/11/laminio-la-ciudad-encontrada-ii.html
Pero,
como ves, yo también voy despacio porque tengo que hilar muy fino. Si
las calculas me gustaría incluirlas (con su correspondiente referencia).
Un saludo.
P.D. De todas maneras, me imagino que las coordenadas te situarán al noreste de Tomelloso...
Calculada la latitud de 39º 55' me resulta, 39º 22' (aproximadamente
Herencia, Alcázar de San Juan, Campo de Criptana, Pedro Muñoz, Las
Mesas, El Provencio, San Clemente...). Lo siento por Alfoldy y
Alhambra, pero como muchos nos tememos, Alhambra es cualquier otra cosa
menos Laminio.
El margen de error +-cinco minutos me da una franja:
Límite norte: Muy cerca y al sur de Consuegra y Madridejos y Las Pedroñeras...
Límite sur: Socuéllamos, Villarrobledo, Minaya...
Sigue sin aparecer Alhambra...
Seamos más condescendientes y ampliemos 10' al norte y al sur. ¿Resultado?
Límite norte: Turleque, Villacañas, La Puebla de Almoradiel, Quintanar de la Orden, Los Hinojosos, Villaescusa de Haro...
Límite sur: Argamasilla de Alba, Santa Marta...
Ni siquiera hemos tocado el término municipal de Alhambra...
Ahora sólo nos falta calcular la longitud, que se lo dejo otra persona ;)
Algunas apreciaciones a vuelapluma:
- El Záncara parece el eje vertebrador
- Coincide bastante cabalmente con la extensión de La Mancha de Vejezate.
- Hay bastantes candidatos arqueológicos -de época prerromana y romana-
por la zona (Vejezate, Los Santos, Cerro de las Nieves, Alcázar, etc...)
Y aquí, algo más que mil palabras:
<a
href="http://img509.imageshack.us/my.php?image=campolaminitanoif9.jpg"
target="_blank"><img
src="http://img509.imageshack.us/img509/2571/campolaminitanoif9.th.jpg"
border="0" alt="Free Image Hosting at www.ImageShack.us" /></a>
Pinchad en la imagen y se ampliará
Vaya, no había dado a código HTML...
Hola Angel, ya terminé de escribir en el artículo, es que la información que obtuve es enorme, y sólo he volcado un bosquejo.
Bueno, vamos a ver creo que te has liado con los grados y minutos
Para 39º 55' tenemos lo siguiente:
1º pasarla a decimal ¡ojo! 39,916666 (dividimos por 60 los minutos)
2º Latitud Real = 36 + (39,91666 - 36) x 91,354 / 111,11 =39,2202º
Ahora si quieres lo pasamos a sexagesimal (yo odio el sexagesimal, pero en fin)
4º 39,2202º (multiplicamos por 60 todo a la dcha de la coma)= 39º 13,21'
Puedes ver por donde te cae, pero el resultado tal cual no vale ya que debe de estar inserto en una interpretación global de otros puntos. De hecho Laminio no está ordenado en las tablas por latitud, quizá esté alterado, hay que hilar más fino, a ver si tengo tiempo..
¡Un saludo!
Ps: He visto tu página: Impresionante y extraordianaria la cantidad de fuentes e información de todo tipo que has reunido reunido sobre esa ciudad : estoy contigo, hay que identificar Laminio.
Huy ¡qué fallo!, no había vuelto a convertir...
Da un poco más al sur: 39º 13' 12
Te has adelantado...
http://www.celtiberia.net/verrespuesta.asp?idp=10620#r64412
Para seguir demostrando el funcionamiento de la fórmula de longitud, vamos a ver el caso de Toletum y Complutum expuesto por Caludioptolomeo en http://www.celtiberia.net/articulo.asp?id=3012
Estas son las coordenas reales y Ptolemaicas:
Complutum 3º 24' 40º 27' 41º 20' 10º 20'
Toletum 39º 51' 4º 1' 40º 45' 9º 25'
| (9,4167 - 10,3333) x Cos(40,7500) x (0,211170217561417 x 40,7500 + 78,3790669888567) / (Cos(39,8500) x 111,325) ) - 3,3667| = 4,0734º= 4º 04,4'
Como se ve en el comentario 14, el resultado es el mismo que el obtenido por Claudioptolomeo tras un cuidadoso cálculo:
Lo hiciste tú. Tomando la división 60.302 : 1423 obtenemos 42´ que al desplazarse desde 3º 22´W nos dan 4º 04´W. Insisto: Toledo
Vamos a ver con otras coordenadas reales para Complutum:
Para Complutum con longitud real de 3º 23' (La de El Juncal)
| (9,4167 - 10,3333) x Cos(40,7500) x (0,211170217561417 x 40,7500 + 78,3790669888567) / (Cos(39,8500) x 111,325) ) - 3,3833| = 4,0901º = 4º 5,4'
Para Complutum con longitud real de 3º 24' (La del cerro de San Juan del Viso)
| (9,4167 - 10,3333) x Cos(40,7500) x (0,211170217561417 x 40,7500 + 78,3790669888567) / (Cos(39,8500) x 111,325) ) - 3,4000| = 4,1068º= 4º 6,4'
Para estos 2 últimos valortes el ajuste buscado con Toletum no se consigue, pues ya para 4º 5,4' tenemos una diferencia con los 4º 1' de Toletum de 4,4' que x 1423 mts son 6.261,2 mts, por encima del margen de 5' que son 5,482 km (a razón de 1096,4 mts)
"Para seguir demostrando el funcionamiento de la fórmula de longitud, vamos a ver el caso de Toletum y Complutum expuesto por Caludioptolomeo en http://www.celtiberia.net/articulo.asp?id=3012
Estas son las coordenas reales y Ptolemaicas:
Complutum 3º 24' 40º 27' 41º 20' 10º 20'
Toletum 39º 51' 4º 1' 40º 45' 9º 25' "
12diviciaco Hoy, a las 16:09 "
Permitidme un pequeño apunte que alivie vuestros cálculos:
... quedan otras pocas, pero si las calculo yo todas, perderían notabilidad vuestras investigaciones.
Un saludo
Pero Sansueña ¿cómo las calculas? yo te cedo toda la notoriedad, a mi me basta con pasarlo bien cuadrando coordenadas y haciendo modestos descubrimientos.
Por cierto que como ya había dicho voy a comprobar las regularidades entre los itinerarios y la Geografia, siguiendo la sugerencia de Fontan, y también voy a seguir dándole vueltas al asunto de las longitudes, claro.
Los resultados, como siempre en breve en su pantalla amiga.
Salud y saludos !
[ 5º____36º____ 12º
[ 5º30'____36º____ 12º
Voy a considerar también el método horario para el cálculo de las longitudes.
De hecho, observa una de las conclusiones de mi estudio, en concreto la gráfica que presento.
El valor en km de un grado de longitud, en la geografía normal, va variando desde el ecuador en función del coseno de la latitud, así: Vº=cos(latitud) x 111,325, siendo 111,325 el valor de un grado de latitud en el ecuador.
Lo que yo observé en la gráfica, es que en la Geographia el grado de longitud varía igual, en función del coseno de la latitud, pero el valor de grado de latitud que hay que aplicar no es constante, sino que varía regularmente (saqué una fórmula precisa) creciendo a medida que lo hace la latitud, según una recta con una inclinación de 12º
Es posible que esto te suene
Saludos
"ABACO DE UNIDADES ANTIGUAS DE MEDIDA" Junio 2006
"La longitud de la circunferencia de la Tierra y nuestras distancias camineras. (IERS)"
- De Erastótenes a Windows: Cómo el reflejo de un rayo de sol, abre numerosas ventanas -
40.075.014,00 Ecuatorial (coseno 1,000019)
40.007.832,00 Polar
111.319,48 Grado
6.395.838,32 Radio
Latitud 00º 00' - Ecuador / Latitud 41º 19 *(Tiermes) 30.092.580,70 - 83.590,50 -(coseno 0,750921)
Milla 1855,32 / * 1393,18
Legua de 15º al grado = 7.421,16 / *Legua de 18.98 al grado = 5.572,70
Estadio 185,53 / * 139,32
Mil pasos (5 pies) = 1546,07 / * 1160,98
Mil brazas (6 pies) = 1855,29 / * 1393,18
"ABACO DE UNIDADES ANTIGUAS DE MEDIDA" Junio 2006
"La longitud de la circunferencia de la Tierra y nuestras distancias camineras. (IERS)"
- De Erastótenes a Windows: Cómo el reflejo de un rayo de sol, abre numerosas ventanas -
A cada latitud le corresponde una longitud y medidas distintas de mayor a menor conforme incrementa la latitud, que trasladado a Ptolomeo cada uno puede elegir su meridiano Oº donde mejor le convenga, yo elegí el 12º por la coincidencia de cada todos sus puntos conocidos y por ser el que divide casi equitativamente Hispania.
Si consultas con A. Cañones - Relojes de Sol y le solicitas que te confeccione un reloj de horas babilónicas para un lugar determinado, no necesitará hacer presencia física para ello, le basta sus coordenadas. De ello supongo se derive que Ptolomeo recopiló la "extensión de las luces y sombras de cada lugar y época y lo trasnformó en latitud y longitud.
http://webs.ono.com/andana
Los expertos en estos temas, supongo podrían averiguar las coordenadas, por la sombra de un edificio, conociendo la orientación del mismo. Recuerda lo que le dijo Don Quijote a Sancho sobre Ptolomeo... y Cervantes debía saber muy bien lo que se decía y a que caminos y lugares se estaba refieriendo... pero lo puso en cristiano ¡ojalá lo hubiese puesto en latín y nos habría ahorrado tiempo.
Por último ríe don Quijote cuando embarcados por el río Ebro, le hacen gracia las simplezas de su escudero al juzgar a Ptolomeo, «Riose don Quijote de la interpretación que Sancho había dado al nombre y al cómputo y cuento del cosmógrafo Ptolomeo» (XXIX).
Y en esto comenzó a llorar tan amargamente, que don Quijote, mohíno y colérico, le dijo:
—¿De qué temes, cobarde criatura? ¿De qué lloras, corazón de mantequillas? ¿Quién te persigue, o quién te acosa, ánimo de ratón casero, o qué te falta, menesteroso en la mitad de las entrañas de la abundancia? ¿Por dicha vas caminando a pie y descalzo por las montañas rifeas , sino sentado en una tabla, como un archiduque, por el sesgo curso deste agradable río , de donde en breve espacio saldremos al mar dilatado? Pero ya habemos de haber salido y caminado por lo menos setecientas o ochocientas leguas; y si yo tuviera aquí un astrolabio con que tomar la altura del polo , yo te dijera las que hemos caminado: aunque o yo sé poco o ya hemos pasado o pasaremos presto por la línea equinocial , que divide y corta los dos contrapuestos polos en igual distancia.
—Y cuando lleguemos a esa leña que vuestra merced dice —preguntó Sancho—, ¿cuánto habremos caminado?
—Mucho —replicó don Quijote—, porque de trecientos y sesenta grados que contiene el globo del agua y de la tierra, según el cómputo de Ptolomeo , que fue el mayor cosmógrafo que se sabe, la mitad habremos caminado, llegando a la línea que he dicho.
—Por Dios —dijo Sancho—, que vuesa merced me trae por testigo de lo que dice a una gentil persona, puto y gafo , con la añadidura de meón, o meo, o no sé cómo.
Rióse don Quijote de la interpretación que Sancho había dado al nombre y al cómputo y cuenta del cosmógrafo Ptolomeo, y díjole:
—Sabrás, Sancho, que los españoles, y los que se embarcan en Cádiz para ir a las Indias Orientales , una de las señales que tienen para entender que han pasado la línea equinocial que te he dicho es que a todos los que van en el navío se les mueren los piojos , sin que les quede ninguno, ni en todo el bajel le hallarán , si le pesan a oro ; y, así, puedes, Sancho, pasear una mano por un muslo, y si topares cosa viva, saldremos desta duda, y si no, pasado habemos.
—Yo no creo nada deso —respondió Sancho—, pero, con todo, haré lo que vuesa merced me manda, aunque no sé para qué hay necesidad de hacer esas experiencias, pues yo veo con mis mismos ojos que no nos habemos apartado de la ribera cinco varas, ni hemos decantado de donde están las alemañas dos varas , porque allí están Rocinante y el rucio en el propio lugar do los dejamos; y tomada la mira, como yo la tomo ahora, voto a tal que no nos movemos ni andamos al paso de una hormiga.
—Haz, Sancho, la averiguación que te he dicho, y no te cures de otra, que tú no sabes qué cosa sean coluros, líneas, paralelos, zodiacos, eclíticas , polos, solsticios, equinocios, planetas, signos, puntos, medidas , de que se compone la esfera celeste y terrestre ; que si todas estas cosas supieras, o parte dellas, vieras claramente qué de paralelos hemos cortado, qué de signos visto y qué de imágines hemos dejado atrás y vamos dejando ahora. Y tórnote a decir que te tientes y pesques, que yo para mí tengo que estás más limpio que un pliego de papel liso y blanco.
He seguido los razonamientos entre Diviciaco y Sansueña porque veo que habeis trabajado el punto de Laminio desde los datos de la Geographia ( Ptol. II, 6, 56) que aporto en la revisión de Carpetania que se cita . Y por ser los que menos garantías me ofrecen , yo solo dire al respecto:
1. Las coordenadas Pt 39º 55´ , 10º 50 no parecen pertenecer a Laminio ( salvo que éste se situase, y me parece que no, al norte de Tomelloso)
2. Las posiciones de Laminio han sido muy discutidas. En J.L. García Alonso, La Península Ibérica en la Geografía de Claudio Ptolomeo , Vitoria, 2003, 325, se recoge una síntesis del estado de la cuestión, y desde luego el punto de Alhambra no se descarta ( quizás por el peso de Alföldy y por el comentario que A. García y Bellido hace en su España del siglo I de nuestra era al referirse a los datos de Plinio ( edición de 1977, p.210, nota 22 ). Otra cosa es que para Alhambra estas coordenadas no coinciden ( cosa que comparto con Angel te Ekiar, aunque insisto en que están alteradas, cambiadas por otras ). Y si hubiera que buscar alguna para encontrar Alhambra (38º 57´r) estas serían 39º 35´Pt , que no existen en el listado de la Carpetania. Eso si: en territorio oretano ( Ptol. II, 6, 58) hay otras posibilidades, pues esta latitud se recoge en el listado. Probaremos.
Saludos. Hasta pronto.
Este artículo sirve como base de pruebas de estos formulones:
http://www.celtiberia.net/articulo.asp?id=3037
Vayamos por partes:
1º Confesar que me sigo perdiendo con el
amigo Claudio, aunque vienen bien vuestras apreciaciones sobre Laminio
que creo, situáis todos en una franja que iría desde el norte de
Tomelloso, hasta el Záncara. Sigo pensando que el punto al que se
refiere, cae en algún lugar de La Mancha de Vejezate. Esto es
importante, porque una entidad posterior (1237) en la que se nombra por
primera vez el topónimo La Mancha, podría ser el buscado y cacareado
Ager Laminitanus. También explicaría otras cuestiones posteriores:
litigios entre la Orden de Santiago y Alcaraz que hicieron adoptar la
salomónica decisión de partir en dos dicho territorio tomando como eje
un camino (posible correspondencia entre A-31 (Liminio- Vejezate) y
A-29 (Lamini- Ruidera)).
2º Claudioptolomeo: combinando la
orientación genérica que ofrece estar situado "al norte de Tomelloso"
con el resto de informaciones que tenemos acerca de Laminio, empiezan a
cuadrar mucho más las cosas que si aceptamos, mansamente, que un
municipium como Alhambra (que honra a los galerios, sus indígenas
tienen nombres iberos, parece tener un collegium potente -cosa más
común en época augustea-, y donde se consideran falsos los únicos
epígrafes que nos situan en época flavia) es Laminium, por mucho circo
romano que tenga sepultado bajo la N-430. No sabía que es un criterio
importante tener circo para llamarse Laminio; de hecho Roma, Toledo,
Cartagena, Mérida (por decir unas pocas) tienen circo y no se llaman
Laminio... No perdamos el norte, por mucho que pensemos que Laminium
era la mismísima Roma rediviva no tenemos referencias a que tuviera
circo... a no ser que la ubiquemos, excavemos y lo encontremos
Hola Angel, ya lo tengo calculado aquí:
http://www.celtiberia.net/articulo.asp?id=3037
He dejado sin interpretar las coordenadas reales obtenidas en función de las ptolemaicas en el recálculo general de la Carpetania para que vosotros las interpretéis
Dime que te parece, cuando puedas...
Escribe aquí (borra esto).
¡¡Qué a gusto se quedaron Caracalla y Ptolomeo!! La Madre que los parió. Seguimos en el tema
Diviciaco, te he contestado a vuelapluma en http://www.celtiberia.net/articulo.asp?id=3037
La justificación la voy escribiendo en el artículo de: http://villarrobledohistorico.blogspot.com/
(Voy lo más rápido que puedo)
Perfecto, porque quiero tener más opiniones sobre los itinerarios y Laminium...
Es que es más complicado Visontium, no basta con aplicar las fórmulas porque las coordenadas pueden estar alteradas, hay que estudiar el tema, buscar un eje referencial, ordenar las coordenadas....un buen trabajo que ahora no voy a hacer, pero para respoder a tu pregunta y no irme por las ramas, si realmente Visontium estaba donde hoy está Vinuesa, se me ocurre que puede que Segisamun lleve sus coordenadas, pero sólo es una suposición a vuelapluma:
Latitud real = 36º + (43,1667º - 36º) x 91,354 / 111,11 = 41,8924º = 41º 53,54'
(desde Cauca)
Longitud real = |( (12,0000º - 10,0000º) x Cos(43,1667º) x (0,211170217561417 x 43,1667º + 78,3790669888567) / (Cos(41,8924º) x 111,325) ) - 4,5170º| = 2,9769º = 2º 58,61'
Aquí tienes más información:
http://www.webs.ulpgc.es/vegueta/downloads/03-065-087.pdf
Saludos y gracias por tu interés.
Hay 34 comentarios.
1