Introducción

Este artículo surge a raiz de una conversación que mantuve con el druida Goudineau.5, en el foro Intercatia acerca de la posible ubicación de la Intercatia vaccea.

Entonces yo apuntaba que una posible vía de solución sería buscar aquel emplazamiento que tuviese un mejor encaje geográfico con la posición que nos dan las tablas de Ptolomeo y para ello aconsejaba leer atentamente esta tesis, donde se manejaban problemas muy parecidos:

Carpetanos y vettones en la Hispania de Ptolomeo: Ciudades y vías romanas de Carpetania y Vettonia de Jesús Montero Vitores (2000).

Se puede desacargar en pdf de aqui: http://www.ucm.es/eprints/2317/

Voy a hacer un rápido resumen, de los aspectos que me han parecido más práctictos y clarificadores de la teoría geográfica de Ptolomeo, de acuerdo a la exposición de Jesús Montero Vítores y según yo lo he entendido:

Resumen de la tesis de referencia

La interpretación de los datos de Ptolomeo tiene su clave, según E. Martínez Hombre, en la proyección Mercator que adapta el valor de grado de latitud, disminuyéndolo conforme se acerca al ecuador, tal y como hacen los mapas del Instituto Geográfico.

Para determinar el valor de grado sobre Hispania, Martínez Hombre utilizó el paralelo 36º, que pasa por Tarifa, coincidente en la geografía actual y en la de Ptolomeo y el paralelo 45 º, latitud de Lucus Asturum, mediando 9º ptolemaicos de diferencia.

La latitud real de Sta María de Lugo es de 43º 26', lo que supone una diferencia de  7º 26' respecto al paralelo 36.

Podemos pasar esta diferencia minutos, multiplicándola por el valor de grado de latitud real  - 111,11 kms - y dividiéndola por 60 obtendremos la distancia real en kilómetros que separa  los paralelos de Sta María de Lugo y Tarifa:

7º 26' = 446' = 446' x 111,11 kms : 60  = 825,92 kms

Como en la geografía de Ptolomeo existía una diferencia de 9º, el valor de grado ptolemaico para Hispania sería de:

825,92 kms : 9 = 91,768 kms.

Además,  Martínez Hombre calculó el valor de grado de latitud en una proyección cónica Mercator, cifrándola en 91,354 kms. no muy diferente de la anterior y que es aplicable uniformemente entre los 30º y 60º, área que comprende la península ibérica.

Con este valor pudo construir una tabla de equivalencias de latitudes, con sus longitudes correspondientes en cada paralelo, ptolemaicas y reales para Hispania. El valor de la longitud es menor cuanto más septentrional es la latitud, como corresponde a una proyección de Mercator.

J M Solana estableció un método para determinar el grado de latitud, que al contrario que Martínez Hombre no consideraba homogéneo, y que se puede resumir en lo siguiente:

a) Tomar la latitud real del núcleo conocido y obtener la diferencia con el paralelo 36 (Hispania está entre los paralelos 36 y 45), reduciéndola a minutos de grado.
b) Se multiplican estos minutos de grado por el valor de grado de latitud real - 111,11 - km para obtener la distancia en kilómetros.
c) Se toma la latitud Ptolemaica del mismo núcleo, se halla la diferencia con el paralelo 36 y se pasa a minutos de grado.
d) Se dividen los kilómetros obtenidos por los minutos Ptolemaicos y se obtiene un valor de grado en kilómetros a comparar con el valor medio de la tabla.

Por otra parte Ptolomeo se fundamenta en la tierra de Posidonio, que con 160.000 estadios de circunferencia era más pequeña que la de Erastóstenes, así el ecúmene ptolemaico comprendía ochenta grados de latitud de norte a sur y ciento ochenta grados de longitud de este a oeste.

Teniendo en cuenta que el grado de Posidonio era de 500 estadios olímpicos, podemos obtener los valores de grado y minuto de latitud teóricos:

1º = 500 x 184,8125 =92,406 Kms.

1' = 92,406 : 60 = 1.540 mts

En la tabla de Martínez Hombre el minuto de longitud entre las coordenadas 45º 45' y 36 º que enmarcan Hispania aumenta en un metro por cada 5 minutos de latitud (Ptolomeo cuenta de cinco en cinco minutos)  con lo cual el minuto se va a mantener en ese intervalo entre los 1026 y 1162 mts, es decir en un valor torno al kilómetro.

Asumiendo que la variación de la longitud en el intervalo de latitud de Hispania es reducida, podemos construir una equivalencia:
si:

   Para  1.851  mts      corresponden 1.540 mts
   para  1.350  mts     corresponden        x

   x=1.123 mts.

 Si el valor medio de latitudes ptolemaicas es de 1.540, el de longitudes será entonces de 1.123 mts

Esta unidad (1.540 mts) resulta aceptable por ser muy próxima al valor de la villa romana, que define la red viaria (los datos de la geografia proceden en gran parte de itinerarios), se aproxima a la milla olímpica de Foucherol (1.542,985 mts) y no resulta muy distinta del valor del minuto de latitud que se obtiene del valor de grado propuesto por Martínez Hombre 91,354  : 60 =1.522,56 mts.

Estos dos valores de minuto de latitud  (1.540 mts) y longitud (1.123) son los utilizados por el autor como punto de partida para interpretar los datos de los núcleos carpetanos y vetones de la geografia de Ptolomeo y serán también los que yo utilizaré para este artículo.

Para la interpretación de los datos de Ptolomeo se nos presenta un problema adicional, que es el de la inclinación de los ejes de referencia, problema ya mencionado por Estrabón(III,1,23), problema que condujo a la declinación de ejes realizada por L. Monteagudo para hacer coincidir puntos en Galicia.

J. Larrañaga cifró la diferencia entre el polo actual y el de Ptolomeo en 13º 37', siendo esta inclinación verificable en varios centenares de casos en la península ibérica (pag 104)

Hasta aquí esta introducción, en la que me he limitado a resumir y condensar lo expuesto en el capítulo II de la tesis.

Metodología aplicable

Para  el aspecto eminentemente práctico que nos ocupa, la construcción de una metodología que nos permita efectuar una correspondencia entre las posiciones de núcleos de los vacceos tal y como son citadas por Ptolomeo en sus tablas geográficas y las coordenadas geográficas modernas, propongo el siguiente método:

1- Buscaremos un núcleo suficientemente conocido, cuyo valor de grado de latitud según el método de J.M. Solana, se adapte al valor de grado de 91,354 kms, para constituir una referencia fiable.

2- Buscaremos otro núcleo cuya ubicación real también conozcamos razonablemente y calcularemos tanto las distancias reales como las ptolemaicas al paralelo de referencia, y comprobaremos igualmente su valor de grado.

Como es de esperar que las distancias reales y ptolemaicas no coincidan, procederemos a declinar los ejes de referencia exáctamente 13º en dirección S-W, coherentemente con la cifra de J. Larrañaga, y comprobaremos entonces si hay coincidencia.

3 -En caso afirmativo buscaremos un tercer núcleo que figure en las tablas de Ptolomeo, de posición real aceptablemente conocida, y repetiremos los pasos 2 y 3. Esto servirá como comprobación adicional de la alineación del eje de coordenadas centrado en el primer punto.

4- En caso de que todos los puntos hayan sido resueltos de forma satisfactoria, podemos intentar posicionar algún lugar citado en las tablas y de incierta ubicación, probando sucesivamente con las posiciones de aquellos lugares que se vengan postulando como candidatos, hasta obtener un valor de distancia coherente. Allí donde se dospeche una alteración en los códices, se prodrá probar con las coordenadas de núcleos que se supongan cambiadas.

Con este método únicamente valoraremos el dato de la coherencia de la distancia entre paralelos, dejando un poco de lado el valor de la longitiud, pero en realidad  las longitudes son calculadas por Ptolomeo en función de datos de viajeros y mediciones en tierra, como afirma el autor del trabajo (p. 69), citando a Rey Pastor. En consecuencia consideraremos las longitudes menos significativas y buscaremos sólo la coincidencia de valores de latitud.

Adicionalmente podemos deducir una fórmula que nos permita comprobar si existe coincidencia de distancia entre los paralelos de dos núcleos,  de tal manera que no precisemos representar sobre cuadrícula la declinación.

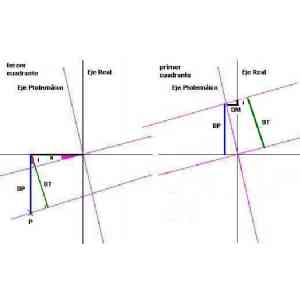
En este esquema vemos en malva el ángulo de declinación a de 13º y los ejes ptolemaicos, declinados en dirección S-W,
DM es la longitud real entre meridianos, DP es la distancia real entre paralelos, P es el núcleo con el que trabajamos y
DT es la distancia Ptolemaica entre paralelos.

En malva estan los ángulos de 13º y en amarillo los de 90.

Podemos ver que

i=Sen(a) x DM
Cos(a)=(i+DT)/DP

Realizando sustituciones:

DT=DP x Cos(a) - DM x Sen(a)

Para el caso de puntos situados en el primer cuadrante se obtiene:

Cos(13)=DT/(DP+i)

Tg(13)=i/DM

DT=DP x Cos(a) +DM x Sen(a)

Se puede comprobar el funcionamiento de esta fórmula con el modelo de declinación que da Jesús Montero Vitores en las páginas 138 y 139, para el caso de Salmantica y Capara.
Como en esas páginas no se ofrecen las coordenadas completas de SALAmanca y Ventas de Caparra, faltando los datos de longitud, deberemos buscarnos esas coordenadas:

SALAmanca tiene unas coordenas de 40,9670 grados de latitud y 5,6500 grados de longitud.

Asimismo el yacimiento arqueológico de Capara está situado a 40º 10' 5.31'' y 6º 5' 32.38''

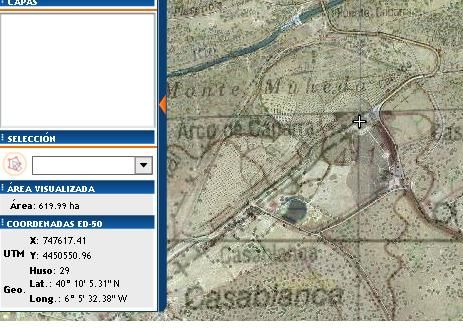
Para operar con las mismas medidas, lo pasamos a grados
40º 10' 5.31 '' =40,1681º
6º 5' 32.38''=6,0923º

Calculamos la diferencia en minutos entre paralelos y la multiplicamos por el valor en kilómetros del minuto de latitud real: 1.851

DP = 40,9670 - 40,1681 = 0,79884 x 60  = 47,9315'  x  1.851 = 88,72  (Jesús Montero Vitores, operando con valores de posición ligeramente distintos, obtiene 87 km)

Calculamos la diferencia en minutos entre meridianos y la multiplicamos por el valor en kilómetros del minuto de longitud real: 1.350:

DM = 6,0923 - 5,6500 = 0,4423 x 60 = 26,539'  x 1.350 = 35,82
 
Aplicamos la fórmula:

DT = 88,72  x Cos(13) - 35,82 x Sen(13) = 78,38

Valor aproximado a la distancia que se obtiene multiplicando la diferencia en minutos de las latitudes por el valor en kilómetros del minuto de latitud ptolemaica: 1.540

41º 50' (Salmantica)  - 41º (Capara) = 50'  ;       50' x 1.540  = 77 km

Determinación del eje de referencia

1)

Tomo una ciudad de emplazamiento bien conocido:

Cauca        

Latitud Ptolemaica       42º 20
Longitud Ptolemaica    10º  

Coca
Latitud real    41,217°
Longitud real  4,517°

Valor de grado:

a)  41,217 - 36º = 5,217º = 313,02'
b)  313,02  x  111,11 = 34.779,6522 km
 
c) 42º 20' - 36º =  380'
d) 34.779,6522  :  380  = 91,525 ~ 91,3542)

2) Será Lucus Asturum, Lugo de Llanera. 

Latitud Ptolemaica       45º

Longitud Ptolemaica    11º 

Lugo de Llanera

Latitud real    43,4412º

Longitud real  5,81812º

Valor de grado:

a)  43,4412 - 36º =7,4412º= 446,472'

b)  446,472' x  111,11 = 49.607,50 km

c) 45º  - 36º = 9º = 540'

d) 49.607,50 :  540'  = 91,865~ 91,354

Vemos que el primer punto se adapta bien al valor de grado medio, así como el segundo punto, con lo cual no habría necesidad de corregir los ejes, en consonancia con lo expuesto por el autor de la tesis de referencia en el punto 2 de la página 151.Calculamos la distancia entre las latitudes reales de ambos puntos:

DP =43,4412- 41,217  = 2,2242x 60  =66,879'  x  1.851 =247,01 km

Calculamos la distancia entre las longitudes reales de ambos puntos:

DM = 5,81812-  4,517  = 1,30112 x 60 = 78,0672 x 1.350 =105,39

Aplicamos la fórmula de declinación:

DT =247,01 x Cos(13) - 105,39x Sen(13) = 264,39

Comparamos este resultado con la distancia entre latitudes ptolemaicas:

45º ' - 42º 20' =  160,02'  ; 160,02' x 1.540  = 246,43 km

Cantidad que difiere en poco mas de medio kilómetro, menos de 1 minuto de grado con la distancia real, evidenciando la inutilidad de declinar los ejes. Como Ptolomeo cuenta de cinco en cinco minutos, la distancia que hemos obtenido declinando los ejes es coherente con la existente entre los paralelos ptolemaicos 45º y 42º 20' y por tanto válida.

3) Vamos ahora a buscar un tercer punto que nos permita confirmar la alineación del eje de referencia centrado en Cauca.

Voy a escoger otra ciudad, Albocela, que se viene identificando con El Alba, en las proximidades de Villalazán, Zamora

 http://traianus.rediris.es/astorga2006/12olmo.pdf

Albocela

Latitud Ptolemaica       42º 40'

Longitud Ptolemaica      9º   5'

El Alba

Latitud real   41,49366º

Longitud real   5,583º

Valor de grado:

a)  41,49366º - 36º = 5,49366º= 329,61'

b)  329,61' x  111,11 = 36.624,03 km

c) 42º 40' - 36º = 400'

d) 36.624,03 :  400'  = 91,56 ~ 91,354

Vemos que el primer punto se adapta bien al valor de grado medio, así como el segundo punto, con lo cual no habría necesidad de corregir los ejes, en consonancia con lo expuesto por el autor de la tesis de referencia en el punto 2 de la página 151.

Calculamos la distancia entre las latitudes reales de ambos puntos:

DP =  41,49366 - 41,217  = 0,27666 x 60  =16,5996'  x  1.851 =30,72 km

Calculamos la distancia entre las longitudes reales de ambos puntos:

DM = 5,583 -  4,517  = 1,066 x 60 = 63,96' x 1.350 = 86,34 km

Aplicamos la fórmula de declinación:

DT = 30,72 x Cos(13) + 86,34 x Sen(13) = 49,36

Comparamos este resultado con la distancia entre latitudes ptolemaicas:

42º 40 ' - 42º 20' = 20'  ; 20' x 1.540  = 30,8 km

Es evidente que no es necesario declinar los ejes, la distancia real entre paralelos es de 30,72 km lo que difiere en 8 metros, ínfima fracción del minuto de grado. Como Ptolomeo cuenta de cinco en cinco minutos, la distancia que hemos obtenido declinando los ejes es coherente con la existente entre los paralelos ptolemaicos 42º 40' y 42º 20' y por tanto válida.

Nota: Véase mi artículo La ubicación de la ciudad vaccea de Pallantia a través de la geografía de Ptolomeo

http://www.celtiberia.net/articulo.asp?id=2916

Allí identifico más núcleos de los vacceos, siguiendo este método, y en todos los casos se confirma la misma alineación de ejes.

4) Ahora que disponemos de un eje de referencia donde se han hecho corresponder satisfactoriamente las coordenadas ptolemaicas de tres núcleos con las coordenadas geográficas reales, podemos ensayar distintos lugares hasta dar con valor coherente para Intercatia.

Intercatia

Latitud Ptolemaica       43º 25'
Longitud Ptolemaica    10º 15'

Montealegre

Latitud real   41,9
Longitud real  4,9

Valor de grado:

a)  41,9 - 36º =5,9º = 354'
b)  354'  x  111,11 = 39.332,94 km
 
c) 43º 25' - 36º = 445'
d)  39.332,94  :  445'  = 88,38 <> 91,354

Difiere bastante con el valor medio, tenemos la necesidad de corregir los ejes.

Calculamos la distancia entre las latitudes reales de ambos puntos:

DP = 41,9 - 41,217  = 0,683 x 60  =40,98'  x  1.851 =75,85 km

Sin embargo como la distancia Ptolemaica es mayor, se evidencia un problema, pues la distancia ptolemaica ha de ser siempre menor, pues el orbe ptolemaico es menor que el real (pag 138 de la tesis de referencia) , por tanto no es posible declinar los ejes en coherencia con el eje de referencia que hemos comprobado que no precisaba de declinación; por tanto debemos descartar Montealegre:

43º 25 ' - 42º 20' =  64,9'  ; 64,9' x 1.540  = 100,09 km

Ceinos

Intercatia

Latitud Ptolemaica       43º 25'
Longitud Ptolemaica    10º 15'

Ceinos

Latitud real   42,033
Longitud real 5,15

Valor de grado:

a)  42,033 - 36º =6,033º = 361,98'
b)  361,98'  x  111,11 =40.219,5978 km
 
c) 43º 25' - 36º = 445'
d)  40.219,5978  :  445'  = 90,38 <> 91,354

Difiere casi un kilómetro con el valor medio, y aunque pudieramos hacer un ajuste de grado, la distancia entre paralelos reales difiere en más de 24 kilómetros, con respecto a la distancia ptolemaica, lo que aconseja inclinar los ejes:

Calculamos la distancia entre las latitudes reales de ambos puntos:

DP = 41,9 - 41,217  = 0,683 x 60  =40,98'  x  1.851 =75,85 km

Sin embargo como la distancia Ptolemaica es mayor, se evidencia un problema, pues la distancia ptolemaica ha de ser siempre menor, pues el orbe ptolemaico es menor que el real (pag 138 de la tesis de referencia) , por tanto no es posible declinar los ejes en coherencia con el eje de referencia que hemos comprobado que no precisaba de declinación; por tanto debemos descartar Ceinos:

43º 25 ' - 42º 20' =  64,9'  ; 64,9' x 1.540  = 100,09 km

Bolaños de Campos

Intercatia

Latitud Ptolemaica       43º 25'
Longitud Ptolemaica    10º 15'

Bolaños de Campos

Latitud real   42,0
Longitud real 5,283

Valor de grado:

a)  42 - 36º =6º = 360'
b)  360'  x  111,11 =39.999,6 km
 
c) 43º 25' - 36º = 445'
d)  39.999,6  :  445'  =89,88 <> 91,354

Difiere bastante con el valor medio, tenemos la necesidad de corregir los ejes.
Comparamos este resultado con la distancia entre latitudes ptolemaicas:

Calculamos la distancia entre las latitudes reales de ambos puntos:

DP = 42 - 41,217  = 0,783 x 60  =46,98'  x  1.851 =86,959 km

Sin embargo como la distancia Ptolemaica es mayor, se evidencia un problema, pues la distancia ptolemaica ha de ser siempre menor, pues el orbe ptolemaico es menor que el real (pag 138 de la tesis de referencia) , por tanto no es posible declinar los ejes en coherencia con el eje de referencia que hemos comprobado que no precisaba de declinación; por tanto debemos Bolaños de Campos:

43º 25 ' - 42º 20' =  64,9'  ; 64,9' x 1.540  = 100,09 km

Villalpando

Intercatia

Latitud Ptolemaica       43º 25'
Longitud Ptolemaica    10º 15'

Villalpando

Latitud real   41,867
Longitud real 5,4

Valor de grado:

a)  41,867-36º =5,867º = 352,02'
b)  352,02'  x  111,11 = 39.112,9422 km
 
c) 43º 25' - 36º = 445'
d)  39.112,9422  :  445'  =87,89 <> 91,354

Difiere bastante con el valor medio, tenemos la necesidad de corregir los ejes.

Calculamos la distancia entre las latitudes reales de ambos puntos:

DP = 41,867 - 41,217  = 0,65 x 60  =39'  x  1.851 =72,189 km

Sin embargo como la distancia Ptolemaica es mayor, se evidencia un problema, pues la distancia ptolemaica ha de ser siempre menor, pues el orbe ptolemaico es menor que el real (pag 138 de la tesis de referencia) , por tanto no es posible declinar los ejes en coherencia con el eje de referencia que hemos comprobado que no precisaba de declinación; por tanto debemos descartar Villalpando:

43º 25 ' - 42º 20' =  64,9'  ; 64,9' x 1.540  = 100,09 km

Aguilar de Campos

Intercatia

Latitud Ptolemaica       43º 25'
Longitud Ptolemaica    10º 15'

Aguilar de Campos

Latitud real   41,983
Longitud real 5,183

Valor de grado:

a)  41,983-36º =5,983º = 358,98'
b)  358,98'  x  111,11 = 39.886,2678 km
 
c) 43º 25' - 36º = 445'
d)  39.886,2678  :  445'  =89,63 <> 91,354

Difiere bastante con el valor medio, tenemos la necesidad de corregir los ejes.

Calculamos la distancia entre las latitudes reales de ambos puntos:

DP = 41,983 - 41,217  =0,766 x 60  =45,96'  x  1.851 =85,07 km

Sin embargo como la distancia Ptolemaica es mayor, se evidencia un problema, pues la distancia ptolemaica ha de ser siempre menor, pues el orbe ptolemaico es menor que el real (pag 138 de la tesis de referencia) , por tanto no es posible declinar los ejes en coherencia con el eje de referencia que hemos comprobado que no precisaba de declinación; por tanto debemos descartar Aguilar de Campos:

43º 25 ' - 42º 20' =  64,9'  ; 64,9' x 1.540  = 100,09 km

Paredes de Nava

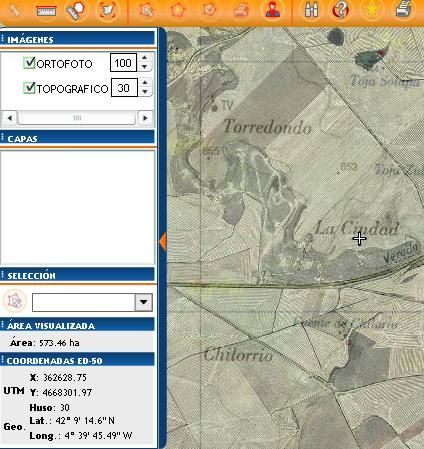
Intercatia

Latitud Ptolemaica       43º 25'
Longitud Ptolemaica    10º 15'

Paredes de Nava, pago de La Ciudad

Latitud real    42,15405 º
Longitud real  4,66263º

Valor de grado:

a)  42,15405 - 36º =6,15405º = 369,243'
b)  369,243'  x  111,11 = 41.026,58973 km
 
c) 43º 25' - 36º = 445'
d) 41.026,58973  :  445'  = 92,19454 ~  91,354

Es posible hacer una adaptación al valor de grado, suponiendo 4 minutos más a la latitud de Ptolomeo 41.026,58973  :  449'=91,372

El valor de grado es adecuado, sin embargo la distancia real con el paralelo de Cauca difiere en unos 4 kilómetros con respecto a las latitudes ptolemaicas, como veremos, por tanto podemos intentar un mejor ajuste, declinando los ejes:

Calculamos la distancia entre las latitudes reales de ambos puntos:

DP = 42,15405 - 41,217  = 0,93705 x 60  =56,223'  x  1.851 =104,068 km

Calculamos la distancia entre las longitudes reales de ambos puntos:

DM = 4,66263-  4,517  =0,14563 x 60 = 8,7378'  x 1.350 =11,79603
 
Aplicamos la fórmula de declinación:

DT =104,068  x Cos(13) + 11,79603 x Sen(13) = 104,05

Comparamos este resultado con la distancia entre latitudes ptolemaicas:

43º 25 ' - 42º 20' =  64,9'  ; 64,9' x 1.540  = 100,09 km

La distancia real difiere con la Ptolemaica en 3,978 km, es decir menos de 3 minutos de grado. Como Ptolomeo cuenta de cinco en cinco minutos, la distancia que hemos obtenido sin declinar los ejes es coherente con la existente entre los paralelos ptolemaicos 43º 25' y 42º 20' y por tanto válida.

Pero además la distancia obtenida declinando los ejes, si fuese posible encontrar un núcleo de los vacceos que formase con Cauca un vector inclinado 13º como muchos puntos en Hispania (hasta 447 casos en la península ibérica pag 104 de la tésis de referencia y conforme a los datos de L. Monteagudo y J. Larrañaga), da una diferencia con la ptolemaica ligeramente menor, 3,96 km,  Por todo lo cual la ciudad vaccea de Intercatia ofrece un perfecto ajuste con los datos de latitud de las tablas de Ptolomeo si la suponemos ubicada en Paredes de Nava, en el pago denominado la Ciudad o área circunvecina.

Enlaces

Carpetanos y vettones en la Hispania de Ptolomeo: Ciudades y vías romanas de Carpetania y Vettonia de Jesús Montero Vitores (2000).

http://www.ucm.es/eprints/2317/

He utilizado esta página para obtener las coordenadas geográficas de una localidad, simplemente introduciendo su nombre:
http://www.heavens-above.com/

También utilizé el Sigpac:
http://sigpac.mapa.es/fega/visor/

Las tablas de Ptolomeo fueron consultadas en esta dirección:
http://penelope.uchicago.edu/Thayer/E/Gazetteer/Periods/Roman/_Texts/Ptolemy/2/5*.html

En este trabajo se identifican algunas ciudades vacceas

http://traianus.rediris.es/astorga2006/12olmo.pdf

Este artículo mio en Celtiberia prosigue con la identificación de núcleos vacceos, siguiendo el mismo procedimiento:

http://www.celtiberia.net/articulo.asp?id=2916

En otro de mis artículos de Celtiberia se obtienen las fórmulas de declinación para el 2º cuadrante:

http://www.celtiberia.net/articulo.asp?id=2918

Escribe aquí el segundo bloque de texto de tu artículo