Introducción

Con este trabajo voy a demostrar que la Geographia es regular, correspondiéndose significativamente las coordenadas de sus núcleos con la geografía real y que esa correspondencia puede hacerse mediante las funciones de transformación que he deducido de las tablas de Martínez Hombre y J. Montero Vítores (1)

Para este propósito utilizaremos una serie de ciudades antiguas, de emplazamiento bien conocido en una comunidad determinada y utilizaremos la lista de coordenadas que la Geographia nos proporciona para esa comunidad, que serán interpretadas mediante las funciones de transformación para localizar dichas ciudades.

Demostraremos que los resultados obtenidos no se deben al azar y que, en consecuencia, la Geographia presenta regularidad y contiene información cartográfica válida, información que es posible extraer con las funciones de transformación.

Entorno de la prueba

El área que vamos a utilizar para esta demostración es la de los CALLAICI LUCENSES. (2)

En primer lugar estableceremos una lista de ciudades de los galaicos identificadas en dicha área; no se considerarán ciudades de los astures como Nemetobriga, ni aquellas galaicas del Convento Barcarense: Nos centraremos en los galaicos lucenses y en la lista de ellos de la Geographia, para así ubicar y clarificar el entorno y las condiciones de la prueba.

Las ciudades son las siguientes:

F.Brigantius       A Coruña
Ocelum             Chao Samartín  (Grandas de Salime)
Burum              Area Pobra de Burón
Lucus Augusti    Lugo
Iria Flavia         Iría (Padrón)
Aquis Celenis     Caldas de Reis
Dactonium         Monforte de Lemos

En total son siete. Se han escogido aquellas ciudades de emplazamiento conocido, o al menos que pueda ser establecido en un sector lo suficientemente definido, como para saber si las coordenadas que hemos generado apuntan a dicha área.

Por otra parte tomaremos las coordenadas de las ciudades de los Galaicos Lucenses (Geographia, 2,5), y no incluiremos las listas específicas de accidentes geográficos: ríos, islas y promontorios pues, como se ha dicho, la prueba se hará con las ciudades.

Burum  
Olina 
Vica 
Libunca
Pintia 
Caronium 
Turuptiana  
Glandomirum 
Ocelum 
Turriga   
Iria Flavia  
Lucus Augusti  
Flavius Brigantius  
Aqua Calida  
Dactonium  
Flavia Lambris  
Portus Artabri  
Claudiomerum
Novium
Talamina

Son veinte en total. Los 48º 30' de Olina parecen un error de transcRIPción, con lo que dejaremos la lista en 19 ciudades.

El método: Reductio ad absurdum

Voy a utilizar un método muy empleado por matemáticos griegos como Euclides como pequeño homenaje y desagravio a su conocimiento matemático, astronómico y geográfico, tan puesto en duda con las críticas a la validez de la Geographia de Ptolomeo: la reducción al absurdo.

Para ello asumiremos que los críticos de la Geographia y de los métodos de Martínez Hombre, de  J. Montero y de mis transformaciones están en lo cierto y que en realidad no resulta posible hacer corresponder las coordenadas de las ciudades de la lista anterior con la geografía real.

En definitiva estos críticos presuponen que si señalamos al azar un punto del territorio a considerar, no habrá diferencia a señalarlo con mis ecuaciones (o con los algoritmos de J. Montero) y así las identificaciones que señalamos como válidas dentro del margen de 5' ptolemaicos han sido simples casualidades.

Vamos a comprobar si es esto es cierto:

Supondremos que los datos generados por las funciones son aleatorios y que no se corresponden con las posiciones reales. No obstante supondremos que los resultados obtenidos de aplicar las fórmulas a los valores dados por Ptolomeo a los núcleos galaicos son aleatorios, pero circunscritos al área de los galaicos, pues de lo contrario sería extremadamente improbable dar con alguna ciudad de ellos por casualidad. Como vimos esto no es exáctamente así, pero lo supondremos para ponernos en el caso más favorable posible a la hipótesis aleatoria (a)

Vamos a ver como delimitamos el área de estudio:

El límite sur de los Galaicos Lucenses , comúmente establecido en el río Lérez, está a 42º 25' reales, el límite norte podemos establecerlo en los 43º 41' de Ortigueira.

El límite por el oeste sería Fisterra 9º 16'  y por el este podemos fijarlo en el Esva-Canero 6º 28', un poco más al este del Navia, al existir epigrafía de los albiones al este del Navia y en coincidencia con la opinión de Santos Yanguas (3)

las posiciones las tomaremos de las generadas por las fórmulas de transformación, con precisión hasta el medio minuto, redondeando el resultado al valor más próximo, como se hace en las localizaciones.

Como los posicionamientos generados se consideran válidos en un entorno de 4' reales en la latitud y 3,5' reales en la longitud (que son 5' ptolemaicos), tenemos que que la cuadrícula geográfica entre 42º 25' y 43º 41' tiene 153 valores, tomados de medio minuto minuto en medio minuto y entre los 9º 16' y 6º 28' hay 340 valores, tomados de idéntica forma. En total hay 153 x 340 = 52.020 posiciones de cuadrícula.

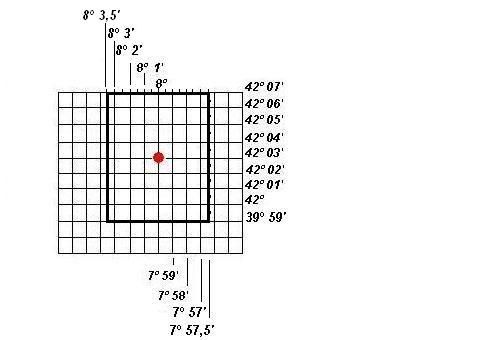
Como vemos en la imagen de arriba, tenemos 17x15 =255 puntos de cuadrícula que podrían considerarse como válidos para localizar una ciudad, siempre forzando al máximo la tolerancia de los 5' ptolemaicos tanto en longitud y latitud, lo que no es el procedimiento habitual, ni es como se ha hecho en el trabajo de los Callaici, pero vamos a ponernos siempre en las condiciones que favorezcan a más no poder a la hipótesis aleatoria (b)

Es decir según la proposición que queremos demostrar debería resultar factible obtener la posición de las 4 ciudades que fueron localizadas en el trabajo de los Callici Lucenses por mera casualidad tras realizar los 19 cálculos efectuados con las ciudades, ya que hay hasta 255 posiciones adecuadas para una ciudad en la cuadrícula.

La probabilidad de obtener una ciudad por causalidad sería P=Casos Favorables/Casos Totales = 255/52.020=0,004901960, es decir 5 entre mil, o lo que es lo mismo: una entre doscientas.

Es decir: la probabilidad de obtener una sóla ciudad al azar en la cuadrícula de los galaicos lucenses, en un único intento, sería la misma que la de extraer una bola determinada de una urna que contuviese 200 bolas.

Siguiendo con el símil podríamos suponer que en esa urna hay 7 bolas blancas y 193 negras.  ¿Cuál sería la probabilidad de extraer una bola blanca en 19 intentos, tantos como la lista de ciudades? ¿y de extraer 2, 3 ó 4  bolas blancas en esos 19 intentos?

Este tipo de problemas pueden resolverse utilizándo lo que se denomina modelo hipergeométrico:

Un modelo hipergeométrico consiste en una variable aleatoria que podemos definir como la cantidad de objetos de tipo A en un muestreo sin reposición de tamaño n en una población de N objetos donde k de ellos son del tipo A. (4)

En nuestro problema N será 200, el nº de objetos de tipo A es k=7 (ciudades conocidas en el área) y el tamaño del muestreo, será n=19 (nº de coordenadas tomadas de los galaicos)

La variable se calculará para i=4, el número de ciudades ciudades de ubicación conocida que hemos obtenido en el área estrictamente galaica: (2)

F.Brigantius      45º           5º 20'pt   Portus Artabri  43º 23'N, 8º 23'W    A Coruña

Ocelum            44º 45'      6º 20'pt  Flavia Lambris  43º 12'N ,6º 55,3'W Chao Samartín

Lucus Augusti   44º 30'      6º 25'pt   Iria Flavia        43º 0'N,   7º 33'W    Lugo

Burum             44º 45'      7º pt      Caronium         43º 8'N,   7º 5'W     A. Pobra Burón

Además como las fórmulas de transformación sólo producen un resultado para cada coordenada ptolemaica, podemos y debemos definir el proceso como un muestreo sin reposición (los objetos no se devuelven a la urna después de extraerlos)

Pues ya sólo nos queda aplicar la fórmula y obtener el resultado:

N= 200;  k=7;  n=19; i=4

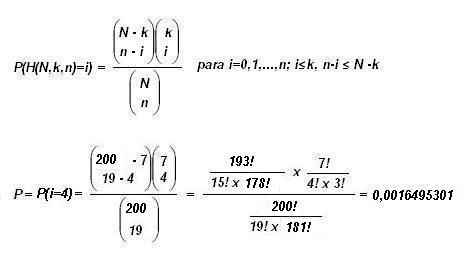(5)

Es decir: la probabilidad de obtener las posiciones de 4 ciudades de 7 en 19 intentos es de 1,65 entre 1000. La probalilidad de obtener tan sólo una ciudad de 7 en 19 intentos es de:

i=1; P=P(i=1)=0,373641224

Ni siquiera podemos esperar tan modesto evento: no llega a 4 entre 10.

El resultado obtenido conduce a una contradicción lógica con la proposición original: Habíamos supuesto que los resultados se debían al azar y sin embargo el resultado obtenido demuestra la improbabilidad de tales resultados, a pesar de asumir siempre las condiciones más favorables para la hipótesis aleatoria (a,b) por lo que hay que rechazarla como falsa, y con ello ya no pueden seguirse sosteniendo tales supuestos,  y hay que asumir como cierta la proposición contraria: que la Geographia presenta auténtica regularidad geográfica con respecto a la geografía real y que las fórmulas y algoritmos la han interpretado correctamente, Q.E.D.

Enlaces

(1) http://www.celtiberia.net/articulo.asp?id=3022
(2) http://www.celtiberia.net/articulo.asp?id=3078#r82482

(3)http://www.ucm.es/BUCM/revistas/ghi/11316993/articulos/CMPL9292120417A.PDF (pag 5)

(4) http://neutron.ing.ucv.ve/electronica/materias/c2508/cap%205.pdf (pag 11 definición 5.5)

(5) Para el cálculo de factoriales elevados es preciso un programa de cálculo simbólico o bibliotecas de funciones para lenguaje C.